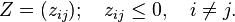the class of Z-matrices are those matrices whose off-diagonal entries are less than or equal to zero; that is, a Z-matrix Z satisfies
Note that this definition coincides precisely with that of a negated Metzler matrix or quasipositive matrix, thus the term quasinegative matrix appears from time to time in the literature, though this is rare and usually only in contexts where references to quasipositive matrices are made.
The Jacobian of a competitive dynamical system is a Z-matrix by definition. Likewise, if the Jacobian of a cooperative dynamical system is J, then (−J) is a Z-matrix.
Related classes are L-matrices, M-matrices, P-matrices, Hurwitz matrices and Metzler matrices. L-matrices have the additional property that all diagonal entries are greater than zero. M-matrices have several equivalent definitions, one of which is as follows: a Z-matrix is an M-matrix if it is nonsingular and its inverse is nonnegative. All matrices that are both Z-matrices and P-matrices are nonsingularM-matrices.