Unitary matrix
From Wikipedia, the free encyclopedia
where In is the identity matrix in n dimensions and  is the conjugate transpose (also called the Hermitian adjoint) of U. Note this condition says that a matrix U is unitary if and only if it has an inverse which is equal to its conjugate transpose
is the conjugate transpose (also called the Hermitian adjoint) of U. Note this condition says that a matrix U is unitary if and only if it has an inverse which is equal to its conjugate transpose 
 is the conjugate transpose (also called the Hermitian adjoint) of U. Note this condition says that a matrix U is unitary if and only if it has an inverse which is equal to its conjugate transpose
is the conjugate transpose (also called the Hermitian adjoint) of U. Note this condition says that a matrix U is unitary if and only if it has an inverse which is equal to its conjugate transpose 
A unitary matrix in which all entries are real is an orthogonal matrix. Just as an orthogonal matrix G preserves the (real) inner productof two real vectors,
so also a unitary matrix U satisfies
If 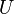 is an n by n matrix then the following are all equivalent conditions:
is an n by n matrix then the following are all equivalent conditions:
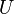 is an n by n matrix then the following are all equivalent conditions:
is an n by n matrix then the following are all equivalent conditions:-
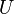 is unitary
is unitary -
 is unitary
is unitary - the columns of
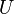 form an orthonormal basis of
form an orthonormal basis of  with respect to this inner product
with respect to this inner product - the rows of
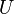 form an orthonormal basis of
form an orthonormal basis of  with respect to this inner product
with respect to this inner product -
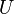 is an isometry with respect to the norm from this inner product
is an isometry with respect to the norm from this inner product -
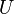 is a normal matrix with eigenvalues lying on the unit circle.
is a normal matrix with eigenvalues lying on the unit circle.



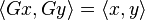

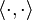 stands now for the standard
stands now for the standard
This site does not show up properly on my iphone 3gs – you may wanna try and fix that
You simply copied a person else’s tale