Modified Richardson iteration

Modified Richardson iteration is an iterative method for solving a system of linear equations. Richardson iteration was proposed by Lewis Richardson in his work dated 1910. It is similar to the Jacobiand Gauss–Seidel method.

We seek the solution to a set of linear equations, expressed in matrix terms as

$A x = b.,$

The Richardson iteration is

$x^{(k+1)} = x^{(k)} + omega left( b - A x^{(k)} right),$

where ω is a scalar parameter that has to be chosen such that the sequence x^(k) converges.

It is easy to see that the method is correct, because if it converges, then $x^{(k+1)} approx x^{(k)}$ and x^(k) has to approximate a solution of Ax = b.

Convergence

Subtracting the exact solution x, and introducing the notation for the error $e^{(k)} approx x^{(k)}-x$ , we get the equality for the errors

e^{(k + 1)} = e^(k) − ωAe^(k) = (I − ωA)e^(k).

Thus,

$|e^{(k+1)}| = |(I-omega A) e^{(k)}|leq |I-omega A| |e^{(k)}|,$

for any vector norm and the corresponding induced matrix norm. Thus, if $|I-omega A|<1$ the method convergences.

Suppose that A is diagonalizable and that (λ_j,v_j) are the eigenvalues and eigenvectors of A. The error converges to 0 if | 1 − ωλ_j | < 1 for all eigenvalues λ_j. If, e.g., all eigenvalues are positive, this can be guaranteed if ω is chosen such that 0 < ω < 2 / λ_max(A). The optimal choice, minimizing all | 1 − ωλ_j | , is ω = 2 / (λ_min(A) + λ_max(A)), which gives the simplest Chebyshev iteration.

If there are both positive and negative eigenvalues, the method will diverge for any ω if the initial error e⁽⁰⁾ has nonzero components in the corresponding eigenvectors.

References

Richardson, L.F. (1910). “The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam”.Philos. Trans. Roy. Soc. London Ser. A 210: 307–357.
Vyacheslav Ivanovich Lebedev (2002). “Chebyshev iteration method”. Springer. Retrieved 2010-05-25. Appeared in Encyclopaedia of Mathematics (2002), Ed. by Michiel Hazewinkel, Kluwer – ISBN 1402006098
Extremal polynomials with application to Richardson iteration for indefinite linear systems (Technical summary report / Mathematics Research Center, University of Wisconsin–Madison)

One thought on “Modified Richardson iteration”

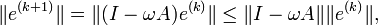
Excellent site. A lot of useful information here. Iˇm sending it to some friends ans also sharing in delicious. And certainly, thanks for your effort!

Comments are closed.