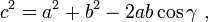Month: February 2011

flops in Matlab

Somebody asked how one may count the number of floating point operations in a MATLAB program.
Prior to version 6, one used to be able to do this with the command flops, but this command is no longer available with the newer versions of MATLAB.
flops is a relic from the LINPACK days of MATLAB (LINPACK has since been replaced by LAPACK). With the use of LAPACK in MATLAB, it will be more approrpiate to use tic andtoc to count elapsed CPU time instead (cf. tic,toc).
If you're interested to know why flops is obsolete, you may wish to read the exchanges in NA digest regarding flops.
Nevertheless, if you feel that you really do need a command to count floating point operations in MATLAB, what you can do is to install Tom Minka's Lightspeed MATLAB toolbox and use the flops counting operations therein.


@cise.ufl.edu>

@cise.ufl.edu>
To count flops, we need to first know what they are.  What is a flop?

LAPACK is not the only place where the question "what is a flop?" is
relevant. Sparse matrix codes are another.  Multifrontal and supernodal
factorization algorithms store L and U (and intermediate submatrices, for
the multifrontal method) as a set of dense submatrices.  It's more
efficient that way, since the dense BLAS can be used within the dense
submatrices.  It is often better explicitly store some of the numerical
zeros, so that one ends up with fewer frontal matrices or supernodes.

So what happens when I compute zero times zero plus zero?  Is that a flop
(or two flops)?  I computed it, so one could argue that it counts.  But it
was useless, so one could argue that it shouldn't count.  Computing it
allowed me to use more BLAS-3, so I get a faster algorithm that happens to
do some useless flops.  How do I compare the "mflop rate" of two
algorithms that make different decisions on what flops to perform and
which of those to include in the "flop count"?

A somewhat better measure would be to compare the two algorithms based an
external count.  For example, the "true" flop counts for sparse LU
factorization can be computed in Matlab from the pattern of L and U as:

        [L,U,P] = lu (A) ;
        Lnz = full (sum (spones (L))) - 1 ;    % off diagonal nz in cols of L
        Unz = full (sum (spones (U')))' - 1 ;  % off diagonal nz in rows of U
        flops = 2*Lnz*Unz + sum (Lnz) ;

The same can be done on the LU factors found by any other factorization
code. This does count a few spurious flops, namely the computation a_ij +
l_ik*u_kj is always counted as two flops, even if a_ij is initially zero.

However, even with this "better" measure, the algorithm that does more
flops can be much faster.  You're better off picking the algorithm with
the smallest memory space requirements (which is not always the smallest
nnz (L+U)) and/or fastest run time.

So my vote is to either leave out the the flop count, or at most return a
reasonable agreed-upon estimate (like the "true flop count" for LU, above)
that is somewhat independent of algorithmic details.  Matrix multiply, for
example, should report 2*n^3, as Cleve states in his Winter 2000
newsletter, even though "better" methods with fewer flops (Strassen's
method) are available.

Tim Davis
University of Florida
davis@cise.ufl.edu@cise.ufl.edu>

x = A b; in Matlab

x = A b;

  1. Is A square?
    no => use QR to solve least squares problem.
  2. Is A triangular or permuted triangular?
    yes => sparse triangular solve
  3. Is A symmetric with positive diagonal elements?
    yes => attempt Cholesky after symmetric minimum degree.
  4. Otherwise
    => use LU on A (:, colamd(A))

x = A \ b; in Matlab

x = A \ b;

  1. Is A square?
    no => use QR to solve least squares problem.
  2. Is A triangular or permuted triangular?
    yes => sparse triangular solve
  3. Is A symmetric with positive diagonal elements?
    yes => attempt Cholesky after symmetric minimum degree.
  4. Otherwise
    => use LU on A (:, colamd(A))

Complexity of Matrix Inversion

What is the computational complexity of inverting an nxn matrix? (In 
general, not special cases such as a triangular matrix.)

Gaussian Elimination leads to O(n^3) complexity. The usual way to 
count operations is to count one for each "division" (by a pivot) and 
one for each "multiply-subtract" when you eliminate an entry.

Here's one way of arriving at the O(n^3) result:

   At the beginning, when the first row has length n, it takes n 
   operations to zero out any entry in the first column (one division, 
   and n-1 multiply-subtracts to find the new entries along the row 
   containing that entry. To get the first column of zeroes therefore 
   takes n(n-1) operations.

   In the next column, we need (n-1)(n-2) operations to get the second 
   column zeroed out.

   In the third column, we need (n-2)(n-3) operations.

   The sum of all of these operations is:

         n            n         n      n(n+1)(2n+1)   n(n+1)
        SUM i(i-1) = SUM i^2 - SUM i = ------------ - ------
        i=1          i=1       i=1           6           2

   which goes as O(n^3). To finish the operation count for Gaussian 
   Elimination, you'll need to tally up the operations for the process 
   of back-substitution (you can check that this doesn't affect the 
   leading order of n^3).

You might think that the O(n^3) complexity is optimal, but in fact 
there exists a method (Strassen's method) that requires only 
O(n^log_2(7)) = O(n^2.807...) operations for a completely general 
matrix. Of course, there is a constant C in front of the n^2.807. This 
constant is not small (between 4 and 5), and the programming of 
Strassen's algorithm is so awkward, that often Gaussian Elimination is 
still the preferred method.

Even Strassen's method is not optimal. I believe that the current 
record stands at O(n^2.376), thanks to Don Coppersmith and Shmuel 
Winograd. Here is a Web page that discusses these methods:

   Fast Parallel Matrix Multiplication - Strategies for Practical 
   Hybrid Algorithms - Erik Ehrling
http://www.f.kth.se/~f95-eeh/exjobb/background.html   

These methods exploit the close relation between matrix inversion and 
matrix multiplication (which is also an O(n^3) task at first glance). 

I hope this helps! 

- Doctor Douglas, The Math Forum
http://mathforum.org/dr.math/

Sparse Finite-Element Matrices in MATLAB

March 1st, 2007

Creating Sparse Finite-Element Matrices in MATLAB

I’m pleased to introduce Tim Davis as this week’s guest blogger. Tim is a professor at the University of Florida, and is the author or co-author of many of our sparse matrix functions (lu, chol, much of sparse backslash, ordering methods such as amd and colamd, and other functions such as etree and symbfact). He is also the author of a recent book, Direct Methods for Sparse Linear Systems, published by SIAM, where more details of MATLAB sparse matrices are discussed ( http://www.cise.ufl.edu/~davis ).

Contents

Optimization problem


1)Airline Optimisation (operations research / linear programming) 

Project Type: $500 – $4,999

Max Bid: Open to fair suggestions
Categories: Writing and translation
Description: 
The airline industry experiences very challenging times, and many airlines need to undertake substantial changes to their business processes to get back to profitability. As Operations of an airline is generally considered a cost driver, there is a big emphasis on cost effectiveness to make improvements to the bottom line. This push towards cost savings is supported by the use of optimization systems that improve the utilization of scarce and expensive resources such as aircraft, crew, gates, etc. To maximize the benefi ts of resource optimization, one needs to identify, model and solve the right operational problems.

We are an airline software development house specialising in aviation solutons specifically for crew and aircraft.
Part of our planned product mix includes mathmatical optimisation solutions that are used to determine ‘best fit’ to a number of competing goals

We want a development partner that can work with us to develope airline optimisation solutions for:
– tail assignment
– crew pairings

These will utilise a number of LP / Column Generation techniques

A good over is at:
http://wwwmaths.anu.edu.au/events/sy2005/odatalks/gordon.ppt

Also take a look at:
– http://www.springerlink.com/content/l0078166515u13u2/
– http://www.crcnetbase.com/doi/abs/10.1201/9781420091878.ch6
–

Our partner needs to understand the maths – we can teach the domain knowledge if needs be !

Deliverables: 1) All deliverables will be considered “work made for hire” under U.S. Copyright law. Employer will receive exclusive and complete copyrights to all work purchased. (No GPL, GNU, 3rd party components, etc. unless all copyright ramifications are explained AND AGREED TO by the employer on the site per the worker’s Worker Legal Agreement).
2) Complete and fully-functional working program(s) in executable form as well as complete source code of all work done.
3) Deliverables must be in ready-to-run condition, as follows (depending on the nature of the deliverables):
a) For web sites or other server-side deliverables intended to only ever exist in one place in the Employer’s environment–Deliverables must be installed by the Worker in ready-to-run condition in the Employer’s environment.
b) For all others including desktop software or software the employer intends to distribute: A software installation package that will install the software in ready-to-run condition on the platform(s) specified in this project.

This broadcast message was sent to all bidders on Monday Feb 7, 2011 11:34:00 PM:

Hi all – we have reactivated this project so please take a look at the Crew Pairings problem initially and let me know if you can help us. We’d be glad to engage !
Platform: C# .NET 4.0 framework potentially based on Microsoft Solver Foundation.

Bidding Ends: 

Approved for posting on 7/19/2010 11:08:29 PM and accessed 1580 times.
     Back to Top

dot product

Vector formulation

The law of cosines is equivalent to the formula
vec bcdot vec c = Vert vec bVertVertvec cVertcos theta
in the theory of vectors, which expresses the dot product of two vectors in terms of their respective lengths and the angle they enclose.

Fig. 10 — Vector triangle

Proof of equivalence. Referring to Figure 10, note that
vec a=vec b-vec c,,
and so we may calculate:
begin{align} Vertvec aVert^2 & = Vertvec b - vec cVert^2 \ & = (vec b - vec c)cdot(vec b - vec c) \ & = Vertvec b Vert^2 + Vertvec c Vert^2 - 2 vec bcdotvec c. end{align}
The law of cosines formulated in this notation states:
Vertvec aVert^2 = Vertvec b Vert^2 + Vertvec c Vert^2 - 2 Vert vec bVertVertvec cVertcos(theta), ,
which is equivalent to the above formula from the theory of vectors.

  1. (by definition of dot product)

    If you think of the length of the 3 vectors |A|,|B| and |B-A| as the lengths of the sides of a triangle, you can apply the law of cosines here too (To visualize this, draw the 2 vectors A and B onto a graph, now the vector from A to B will be given by B-A. The triangle formed by these 3 vectors is applied to the law of cosines for a triangle)

    In this case, we substitute: |B-A| for c, |A| for a, |B| for b
    and we obtain:

  2.   (by law of cosines)

Remember now, that Theta is the angle between the 2 vectors A, B.
Notice the common term |A||B|cos(Theta) in both equations. We now equate equation (1) and (2), and obtain


and hence

(by pythagorean length of a vector) and thus

Law of cosines

Law of cosines

From Wikipedia, the free encyclopedia
This article is about the law of cosines in Euclidean geometry. For the cosine law of optics, see Lambert’s cosine law.

Figure 1 – A triangle. The angles α,β, and γ are respectively opposite the sides a, b, and c.

 
Trigonometry
History
Usage
Functions
Generalized
Inverse functions
Further reading
Reference
Identities
Exact constants
Trigonometric tables
Laws and theorems
Law of sines
Law of cosines
Law of tangents
Pythagorean theorem
Calculus
Trigonometric substitution
Integrals of functions
Derivatives of functions
Integrals of inverse functions
v · d · e
In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) is a statement about a general triangle that relates the lengths of its sides to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states that
c^2 = a^2 + b^2 - 2abcosgamma ,
where γ denotes the angle contained between sides of lengths a and b and opposite the side of length c.
The law of cosines generalizes the Pythagorean theorem, which holds only for right triangles: if the angle γ is a right angle (of measure 90° or π/2 radians), then cos(γ) = 0, and thus the law of cosines reduces to
c^2 = a^2 + b^2 ,
The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known, and in computing the angles of a triangle if all three sides are known.
By changing which legs of the triangle play the roles of a, b, and c in the original formula, one discovers that the following two formulas also state the law of cosines:
a^2 = b^2 + c^2 - 2bccosalpha,
b^2 = a^2 + c^2 - 2accosbeta,
http://en.wikipedia.org/wiki/Law_of_cosines