Author: admin

Successive over-relaxation

Successive over-relaxation

From Wikipedia, the free encyclopedia
In numerical linear algebra, the method of successive over-relaxation (SOR) is a variant of the Gauss–Seidel method for solving alinear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process. It was devised simultaneously by David M. Young and by H. Frankel in 1950 for the purpose of automatically solving linear systems on digital computers. Over-relaxation methods had been used before the work of Young and Frankel. For instance, the method of Lewis Fry Richardson, and the methods developed by R. V. Southwell. However, these methods were designed for computation by human calculators, and they required some expertise to ensure convergence to the solution which made them inapplicable for programming on digital computers. These aspects are discussed in the thesis of David M. Young.[1]

Gauss–Seidel method

Gauss–Seidel method

From Wikipedia, the free encyclopedia
In numerical linear algebra, the Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method used to solve a linear system of equations. It is named after the German mathematicians Carl Friedrich Gauss and Philipp Ludwig von Seidel, and is similar to the Jacobi method. Though it can be applied to any matrix with non-zero elements on the diagonals, convergence is guaranteed if the matrix is either diagonally dominant, or symmetric and positive definite.

Jacobi method

Jacobi method

From Wikipedia, the free encyclopedia
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process is then iterated until it converges. This algorithm is a stripped-down version of the Jacobi transformation method of matrix diagonalization. The method is named after German mathematician Carl Gustav Jakob Jacobi.

Chebyshev iteration method


An iterative algorithm for finding a solution to a linear equation
(1)

that takes account of information about the inclusion of  — the spectrum of the operator  — in a certain set , and uses the properties and parameters of those polynomials that deviate least from zero on  and are equal to 1 at 0.

The most well-developed Chebyshev iteration method is obtained when in (1),  is a linear self-adjoint operator and , where  are the boundary points of the spectrum; then the Chebyshev iteration method uses the properties of the Chebyshev polynomials of the first kind, . For this case one considers two types of Chebyshev iteration methods:
(2)
(3)

in which for a given  one obtains a sequence  as . In (2) and (3)  and  are the numerical parameters of the method. If , then the initial error  and the error at the -th iteration  are related by the formula

where

(4)

The polynomials  are calculated using the parameters of each of the methods (2), (3): for method(2)

(5)

where  are the elements of the permutation , while for method (3)they are calculated from the recurrence relations

(6)

Here

The methods (2) and (3) can be optimized on the class of problems for which  by choosing the parameters such that  in (4) is the polynomial least deviating from zero on . It was proved in 1881 by P.L. Chebyshev that this is the polynomial
(7)

where . Then

(8)

where

Substituting (7) for  in (6), the parameters  of the method (3) are determined:
(9)

where

(10)

Thus, computing  and  by the formulas (9) and (10), one obtains the Chebyshev iteration method (3) for which  is optimally small for each .
To optimize (2) for a given , the parameters  are chosen corresponding to the permutation in formula (5) in such a way that (7) holds, that is,
(11)

Then after  iterations, inequality (8) holds for .

An important problem for small  is the question of the stability of the method (2), (5), (11). An imprudent choice of  may lead to a catastrophic increase in  for some , to the loss of significant figures, or to an increase in the rounding-off errors allowed on intermediate iteration. There exist algorithms that mix the parameters in (11) and guarantee the stability of the calculations: for  see Iteration algorithm; and for  one of the algorithms for constructing  is as follows. Let , and suppose that  has been constructed, then
(12)

There exists a class of methods (2) — the stable infinitely repeated optimal Chebyshev iteration methods — that allows one to repeat the method (2), (5), (11) after  iterations in such a way that it is stable and such that it becomes optimal again for some sequence . For the case , it is clear from the formula
(13)

that  agrees with (11). If after  iterations one repeats the iteration (2), (5), (11) further, taking for  in (11) the  values

(14)

then once again one obtains a Chebyshev iteration method after  iterations. To ensure stability, the set(14) is decomposed into two sets: in the -th set, , one puts the  for which  is a root of the -th bracket in (13); within each of the subsets the  are permuted according to the permutation . For  one substitutes elements of the first set in (5), (11), and for  one uses the second subset; the permutation  is defined in the same way. Continuing in an analogous way the process of forming parameters, one obtains an infinite sequence , uniformly distributed on , called a -sequence, for which the method (2) becomes optimal with  and

(15)

The theory of the Chebyshev iteration methods (2), (3) can be extended to partial eigen value problems. Generalizations also exist to a certain class of non-self-adjoint operators, when  lies in a certain interval or within a certain domain of special shape (in particular, an ellipse); when information is known about the distribution of the initial error; or when the Chebyshev iteration method is combined with the method of conjugate gradients.
One of the effective methods of speeding up to the convergence of the iterations (2), (3) is a preliminary transformation of equation (1) to an equivalent equation of the form

and the application of the Chebyshev iteration method to this equation. The operator  is defined by taking account of two facts: 1) the algorithm for computing a quantity of the form  should not be laborious; and 2)  should lie in a set that ensures the fast convergence of the Chebyshev iteration method.

References

[1]  G.I. Marchuk,   V.I. Lebedev,   “Numerical methods in the theory of neutron transport” , Harwood  (1986)  (Translated from Russian)
[2]  N.S. Bakhvalov,   “Numerical methods: analysis, algebra, ordinary differential equations” , MIR  (1977)  (Translated from Russian)
[3]  G.I. Marchuk,   “Methods of numerical mathematics” , Springer  (1982)  (Translated from Russian)
[4]  A.A. Samarskii,   “Theorie der Differenzverfahren” , Akad. Verlagsgesell. Geest u. Portig K.-D.  (1984)  (Translated from Russian)
[5a]  V.I. Lebedev,   S.A. Finogenov,   “The order of choices of the iteration parameters in the cyclic Chebyshev iteration method”  Zh. Vychisl. Mat. i Mat. Fiz. , 11 : 2  (1971)  pp. 425–438  (In Russian)
[5b]  V.I. Lebedev,   S.A. Finogenov,   “Solution of the problem of parameter ordering in Chebyshev iteration methods”  Zh. Vychisl. Mat. i Mat. Fiz , 13 : 1  (1973)  pp. 18–33  (In Russian)
[5c]  V.I. Lebedev,   S.A. Finogenov,   “The use of ordered Chebyshev parameters in iteration methods”  Zh. Vychisl. Mat. i Mat. Fiz. , 16 : 4  (1976)  pp. 895–907  (In Russian)
[6a]  V.I. Lebedev,   “Iterative methods for solving operator equations with spectrum located on several segments”  Zh. Vychisl. Mat. i Mat. Fiz. , 9 : 6  (1969)  pp. 1247–1252  (In Russian)
[6b]  V.I. Lebedev,   “Iteration methods for solving linear operator equations, and polynomials deviating least from zero” , Mathematical analysis and related problems in mathematics , Novosibirsk  (1978)  pp. 89–108  (In Russian)

Comments

In the Western literature the method (2), (5), (11) is known as the Richardson method of first degree [a2]or, more widely used, the Chebyshev semi-iterative method of first degree. The method goes back to an early paper of L.F. Richardson , where the method (2), (5) was already proposed. However, Richardson did not identify the zeros  of  with the zeros of (shifted) Chebyshev polynomials as done in (11), but (less sophisticatedly) sprinkled them uniformly over the interval . The use of Chebyshev polynomials seems to be proposed for the first time in [a1] and [a3].
The  “stable infinitely repeated optimal Chebyshev iteration methods”  outlined above are based on the identity , which immediately leads to the factorization

This formula has already been used in [a1] in the numerical determination of fundamental modes.

The method (3), (9) is known as Richardson’s method or Chebyshev’s semi-iterative method of second degree. It was suggested in [a9] and turns out to be completely stable; thus, at the cost of an extra storage array the instability problems associated with the first-degree process are avoided.
As to the choice of the transformation operator  (called  “preconditioningpreconditioning” ), an often used  “preconditionerpreconditioner”  is the so-called SSOR matrix (Symmetric Successive Over-Relaxation matrix) proposed in [a8].
Introductions to the theory of Chebyshev semi-iterative methods are provided by [a2] and [a3]. An extensive analysis can be found in [a10], Chapt. 5 and in [a4]. In this work the spectrum of the operator  is assumed to be real. An analysis of the case where the spectrum is not real can be found in [a5].
Instead of using minimax polynomials, one may consider integral measures for  “minimizing”   on . This leads to the theory of kernel polynomials introduced in [a9] and extended in [a11], Chapt. 5.
Iterative methods as opposed to direct methods (cf. Direct method) only make sense when the matrix is sparse (cf. Sparse matrix). Moreover, their versatility depends on how large an error  is tolerated; often other errors, e.g., truncation errors in discretized systems of partial differential equations, are more dominant.
When no information about the eigen structure of  is available, or in the non-self-adjoint case, it is often preferable to use the method of conjugate gradients (cf. Conjugate gradients, method of). Numerical algorithms based on the latter method combined with incomplete factorization have proven to be one of the most efficient ways to solve linear problems up to now (1987).

References

[a1]  D.A. Flanders,   G. Shortley,   “Numerical determination of fundamental modes”  J. Appl. Physics, 21  (1950)  pp. 1326–1332
[a2]  G.E. Forsythe,   W.R. Wasow,   “Finite difference methods for partial differential equations” , Wiley  (1960)
[a3]  G.H. Golub,   C.F. van Loan,   “Matrix computations” , North Oxford Acad.  (1983)
[a4]  G.H. Golub,   R.S. Varga,   “Chebyshev semi-iterative methods, successive over-relaxation methods and second-order Richardson iterative methods I, II”  Num. Math. , 3  (1961)  pp. 147–156; 157–168
[a5]  T.A. Manteuffel,   “The Tchebychev iteration for nonsymmetric linear systems”  Num. Math. , 28 (1977)  pp. 307–327
[a6a]  L.F. Richardson,   “The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam”  Philos. Trans. Roy. Soc. London Ser. A , 210  (1910)  pp. 307–357
[a6b]  L.F. Richardson,   “The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam”  Proc. Roy. Soc. London Ser. A , 83  (1910)  pp. 335–336
[a7]  G. Shortley,   “Use of Tchebycheff-polynomial operators in the numerical solution of boundary-value problems”  J. Appl. Physics , 24  (1953)  pp. 392–396
[a8]  J.W. Sheldon,   “On the numerical solution of elliptic difference equations”  Math. Tables Aids Comp. , 9  (1955)  pp. 101–112
[a9]  E.L. Stiefel,   “Kernel polynomials in linear algebra and their numerical applications” , Appl. Math. Ser. , 49 , Nat. Bur. Standards  (1958)
[a10]  R.S. Varga,   “Matrix iterative analysis” , Prentice-Hall  (1962)
[a11]  E.L. Wachspress,   “Iterative solution of elliptic systems, and applications to the neutron diffusion equations of nuclear physics” , Prentice-Hall  (1966)

Extremal polynomials with application to Richardson iteration for indefinite linear systems (Technical summary report / Mathematics Research Center, University of Wisconsin–Madison)

Modified Richardson iteration

Modified Richardson iteration is an iterative method for solving a system of linear equations. Richardson iteration was proposed by Lewis Richardson in his work dated 1910. It is similar to the Jacobiand Gauss–Seidel method.
We seek the solution to a set of linear equations, expressed in matrix terms as
A x = b.,
The Richardson iteration is
x^{(k+1)} = x^{(k)} + omega left( b - A x^{(k)} right),
where ω is a scalar parameter that has to be chosen such that the sequence x(k) converges.
It is easy to see that the method is correct, because if it converges, then x^{(k+1)} approx x^{(k)} and x(k) has to approximate a solution of Ax = b.


Convergence

Subtracting the exact solution x, and introducing the notation for the error e^{(k)} approx x^{(k)}-x, we get the equality for the errors
e(k + 1) = e(k) − ωAe(k) = (I − ωA)e(k).
Thus,
|e^{(k+1)}| = |(I-omega A) e^{(k)}|leq |I-omega A| |e^{(k)}|,
for any vector norm and the corresponding induced matrix norm. Thus, if |I-omega A|<1 the method convergences.
Suppose that A is diagonalizable and that (λj,vj) are the eigenvalues and eigenvectors of A. The error converges to 0 if | 1 − ωλj | < 1 for all eigenvalues λj. If, e.g., all eigenvalues are positive, this can be guaranteed if ω is chosen such that 0 < ω < 2 / λmax(A). The optimal choice, minimizing all | 1 − ωλj | , is ω = 2 / (λmin(A) + λmax(A)), which gives the simplest Chebyshev iteration.
If there are both positive and negative eigenvalues, the method will diverge for any ω if the initial error e(0) has nonzero components in the corresponding eigenvectors.


References

Fréchet derivative

 the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from functions of one variable to functions on Banach spaces. The Fréchet derivative should be contrasted to the more general Gâteaux derivative which is a generalization of the classical directional derivative.
The Fréchet derivative has applications throughout mathematical analysis, and in particular to the calculus of variations and much of nonlinear analysis and nonlinear functional analysis. It has applications to nonlinear problems throughout the sciences.

Metzler matrix

 a Metzler matrix is a matrix in which all the off-diagonal components are nonnegative (equal to or greater than zero)
qquad forall_{ineq j}, x_{ij} geq 0.
Metzler matrices appear in stability analysis of time delayed differential equations and positive linear dynamical systems. Their properties can be derived by applying the properties of Nonnegative matrices to matrices of the form M + aI where M is a Metzler matrix.

P-matrix

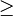a P-matrix is a complex square matrix with every principal minor > 0. A closely related class is that of P0-matrices, which are the closure of the class of P-matrices, with every principal minor geq 0.


Spectra of P-matrices

By a theorem of Kellogg, the eigenvalues of P– and P0– matrices are bounded away from a wedge about the negative real axis as follows:
If {u1,…,un} are the eigenvalues of an n-dimensional P-matrix, then

|arg(u_i)| < pi - frac{pi}{n}, i = 1,...,n
If {u1,…,un}, u_i neq 0, i = 1,…,n are the eigenvalues of an n-dimensional P0-matrix, then

|arg(u_i)| leq pi - frac{pi}{n}, i = 1,...,n

Notes

The class of nonsingular M-matrices is a subset of the class of P-matrices. More precisely, all matrices that are both P-matrices and Z-matrices are nonsingular M-matrices.
If the Jacobian of a function is a P-matrix, then the function is injective on any rectangular region of mathbb{R}^n.
A related class of interest, particularly with reference to stability, is that of P( − )-matrices, sometimes also referred to as N − P-matrices. A matrix A is a P( − )-matrix if and only if ( − A) is a P-matrix (similarly for P0-matrices). Since σ(A) = − σ( − A), the eigenvalues of these matrices are bounded away from the positive real axis.


References

  • R. B. Kellogg, On complex eigenvalues of M and P matrices, Numer. Math. 19:170-175 (1972)
  • Li Fang, On the Spectra of P– and P0-Matrices, Linear Algebra and its Applications 119:1-25 (1989)
  • D. Gale and H. Nikaido, The Jacobian matrix and global univalence of mappings, Math. Ann. 159:81-93 (1965)

Z-matrix

 the class of Z-matrices are those matrices whose off-diagonal entries are less than or equal to zero; that is, a Z-matrix Z satisfies
Z=(z_{ij});quad z_{ij}leq 0, quad ineq j.
Note that this definition coincides precisely with that of a negated Metzler matrix or quasipositive matrix, thus the term quasinegative matrix appears from time to time in the literature, though this is rare and usually only in contexts where references to quasipositive matrices are made.
The Jacobian of a competitive dynamical system is a Z-matrix by definition. Likewise, if the Jacobian of a cooperative dynamical system is J, then (−J) is a Z-matrix.
Related classes are L-matrices, M-matrices, P-matrices, Hurwitz matrices and Metzler matrices. L-matrices have the additional property that all diagonal entries are greater than zero. M-matrices have several equivalent definitions, one of which is as follows: a Z-matrix is an M-matrix if it is nonsingular and its inverse is nonnegative. All matrices that are both Z-matrices and P-matrices are nonsingularM-matrices.