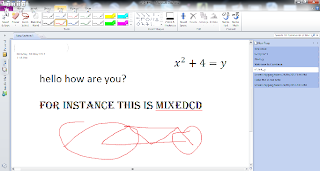Category: teaching
Anki
Anki is a program which makes remembering things easy. Because it’s a lot more efficient than traditional study methods, you can either greatly decrease your time spent studying, or greatly increase the amount you learn.
Anyone who needs to remember things in their daily life can benefit from Anki. Since it is content-agnostic and supports images, audio, videos and scientific markup (via LaTeX), the possibilities are endless.
For example:
- Learning a language
- Studying for medical and law exams
- Memorizing people’s names and faces
- Brushing up on geography
- Mastering long poems
- Even practicing guitar chords!
OpenCPU
An API for Embedded Scientific Computing
OpenCPU is a system for embedded scientific computing and reproducible research.
Free Podcasting Software
A vast array of software is available to support your podcasting requirements; some programs offer one stop integrated solutions to all your podcasting needs, while others fill more specific niches. However, every piece of software that you need in order to record and produce a professional, quality podcast is readily available free of charge.
Acquiring the Audio
No matter what software you choose to help create and produce your podcasts, you will first have to get your audio into the computer. How you choose to do this is entirely up to you, but is likely to depend on what level of audio quality you want and your budget. At the most basic level you could use your computer’s in-built microphone, but for a reasonable degree of quality you will want a semi-decent external microphone.
1. Audacity – Audio Recorder and Editor
2. WinLAME – Audio Encoder
 Once your audio has been recorded and edited (preferably in WAV format) you will need to convert it into a suitable podcast format. The universally accepted audio file format for podcasts is MP3. WinLAME is an excellent piece of free podcasting software designed to convert WAV files into the podcast friendly MP3 format.
Once your audio has been recorded and edited (preferably in WAV format) you will need to convert it into a suitable podcast format. The universally accepted audio file format for podcasts is MP3. WinLAME is an excellent piece of free podcasting software designed to convert WAV files into the podcast friendly MP3 format.
3. Mp3Tag – ID3 Tag Editor
 Now that you have your podcast MP3 audio file and some suitable artwork for its cover, you will need to embed the artwork into the MP3 file and add some additional tags that can be displayed by the listener’s playback device.
Now that you have your podcast MP3 audio file and some suitable artwork for its cover, you will need to embed the artwork into the MP3 file and add some additional tags that can be displayed by the listener’s playback device.
ggplot2
ggplot2 is a data visualization package for the statistical programming language R. Created by Hadley Wickham in 2005, ggplot2 is an implementation of Leland Wilkinson‘s Grammar of Graphics—a general scheme for data visualization which breaks up graphs into semantic components such as scales and layers. ggplot2 can serve as a replacement for the base graphics in R and contains a number of defaults for web and print display of common scales. Since 2005, ggplot2 has grown in use to become one of the most popular R packages.[1][2] It is licensed under GNU GPL v2.[3]
On 2 March 2012, ggplot2 version 0.9.0 was released with numerous changes to internal organization, scale construction and layers.[4] An update dealing primarily with bug fixes was released on 9 May 2012, incrementing the version to 0.9.1.[5]
On 25 February 2014, Hadley Wickham formally announced that “ggplot2 is shifting to maintenance mode. This means that we are no longer adding new features, but we will continue to fix major bugs, and consider new features submitted as pull requests. In recognition this significant milestone, the next version of ggplot2 will be 1.0.0”.[6]
Solved game
A solved game is a game whose outcome (win, lose, or draw) can be correctly predicted from any position, given that both players play perfectly. Games which have not been solved are said to be “unsolved”. Games for which only some positions have been solved are said to be “partially solved”. This article focuses on two-player games that have been solved.
A two-player game can be “solved” on several levels:[1][2]
Ultra-weak
- Prove whether the first player will win, lose, or draw from the initial position, given perfect play on both sides. This can be a non-constructive proof (possibly involving astrategy-stealing argument) that need not actually determine any moves of the perfect play.
Weak
- Provide an algorithm that secures a win for one player, or a draw for either, against any possible moves by the opponent, from the beginning of the game. That is, produce at least one complete ideal game (all moves start to end) with proof that each move is optimal for the player making it. It does not necessarily mean a computer program using the solution will play optimally against an imperfect opponent. For example, the checkers program Chinook will never turn a drawn position into a losing position (since the weak solution of checkers proves that it is a draw), but it might possibly turn a winning position into a drawn position because Chinook does not expect the opponent to play a move that will not win but could possibly lose, and so it does not analyze such moves completely.
Strong
- Provide an algorithm that can produce perfect play (moves) from any position, even if mistakes have already been made on one or both sides.
Despite the name, many game theorists believe that “ultra-weak” are the deepest, most interesting and valuable proofs. “Ultra-weak” proofs require a scholar to reason about the abstract properties of the game, and show how these properties lead to certain outcomes if perfect play is realized.[citation needed]
By contrast, “strong” proofs often proceed by brute force — using a computer to exhaustively search a game tree to figure out what would happen if perfect play were realized. The resulting proof gives an optimal strategy for every possible position on the board. However, these proofs aren’t as helpful in understanding deeper reasons why some games are solvable as a draw, and other, seemingly very similar games are solvable as a win.
Given the rules of any two-person game with a finite number of positions, one can always trivially construct a minimax algorithm that would exhaustively traverse the game tree. However, since for many non-trivial games such an algorithm would require an infeasible amount of time to generate a move in a given position, a game is not considered to be solved weakly or strongly unless the algorithm can be run by existing hardware in a reasonable time. Many algorithms rely on a huge pre-generated database, and are effectively nothing more.
As an example of a strong solution, the game of tic-tac-toe is solvable as a draw for both players with perfect play (a result even manually determinable by schoolchildren). Games like nim also admit a rigorous analysis using combinatorial game theory.
Whether a game is solved is not necessarily the same as whether it remains interesting for humans to play. Even a strongly solved game can still be interesting if its solution is too complex to be memorized; conversely, a weakly solved game may lose its attraction if the winning strategy is simple enough to remember (e.g. Maharajah and the Sepoys). An ultra-weak solution (e.g. Chomp or Hex on a sufficiently large board) generally does not affect playability.
In non-perfect information games, one also has the notion of essentially weakly solved[3]. A game is said to be essentially weakly solved if a human lifetime of play is not sufficient to establish with statistical significance that the strategy is not an exact solution. As an example, the poker variation heads-up limit Texas hold ’em have been essentially weakly solved by the poker bot Cepheus[3][4][5].
Perfect play
In game theory, perfect play is the behavior or strategy of a player that leads to the best possible outcome for that player regardless of the response by the opponent. Based on the rules of a game, every possible final position can be evaluated (as a win, loss or draw). By backward reasoning, one can recursively evaluate a non-final position as identical to that of the position that is one move away and best valued for the player whose move it is. Thus a transition between positions can never result in a better evaluation for the moving player, and a perfect move in a position would be a transition between positions that are equally evaluated. As an example, a perfect player in a drawn position would always get a draw or win, never a loss. If there are multiple options with the same outcome, perfect play is sometimes considered the fastest method leading to a good result, or the slowest method leading to a bad result.
Perfect play can be generalized to non-perfect information games, as the strategy that would guarantee the highest minimal expected outcome regardless of the strategy of the opponent. As an example, the perfect strategy for Rock, Paper, Scissors would be to randomly choose each of the options with equal (1/3) probability. The disadvantage in this example is that this strategy will never exploit non-optimal strategies of the opponent, so the expected outcome of this strategy versus any strategy will always be equal to the minimal expected outcome.
Although the optimal strategy of a game may not (yet) be known, a game-playing computer might still benefit from solutions of the game from certain endgame positions (in the form of endgame tablebases), which will allow it to play perfectly after some point in the game. Computer chess programs are well known for doing this.
Solved games
- Awari (a game of the Mancala family)
- The variant of Oware allowing game ending “grand slams” was strongly solved by Henri Bal and John Romein at the Vrije Universiteit in Amsterdam, Netherlands (2002). Either player can force the game into a draw.
- Checkers
- See “Draughts, English”
- Chopsticks
- The second player can always force a win.[6]
- Connect Four
- Solved first by James D. Allen (Oct 1, 1988), and independently by Victor Allis (Oct 16, 1988).[7] First player can force a win. Strongly solved by John Tromp’s 8-ply database[8](Feb 4, 1995). Weakly solved for all boardsizes where width+height is at most 15[7] (Feb 18, 2006).
- Draughts, English (Checkers)
- This 8×8 variant of draughts was weakly solved on April 29, 2007 by the team of Jonathan Schaeffer, known for Chinook, the “World Man-Machine Checkers Champion“. From the standard starting position, both players can guarantee a draw with perfect play.[9] Checkers is the largest game that has been solved to date, with a search space of 5×1020.[10] The number of calculations involved was 1014, which were done over a period of 18 years. The process involved from 200 desktop computers at its peak down to around 50.[11]
The game of checkers has roughly 500 billion billion possible positions (5 × 1020). The task of solving the game, determining the final result in a game with no mistakes made by either player, is daunting. Since 1989, almost continuously, dozens of computers have been working on solving checkers, applying state-of-the-art artificial intelligence techniques to the proving process. This paper announces that checkers is now solved: Perfect play by both sides leads to a draw. This is the most challenging popular game to be solved to date, roughly one million times as complex as Connect Four. Artificial intelligence technology has been used to generate strong heuristic-based game-playing programs, such as Deep Blue for chess. Solving a game takes this to the next level by replacing the heuristics with perfection.
Flying Logic
Published on Jun 27, 2012
A brief introduction to using Flying Logic. We build a simple transition tree using Flying Logic’s intuitive and efficient interface.
Power and dominance
Non verbal expressions of power and dominance are gestures or motions that assert one´s authority over another.
handshakes
waving
smiling
The colors one wears affect other´s perceptions of one´s authority:
purple: people of high status adorn their clothing with purple to distinguish themselves as noble or wealthy
people attribute greater authority to others wearing red
It is human to strive for power and dominance in social settings
simple gestures establish authority
A firmer handshake
Better posture
Causing slight interruptions in conversation
can rise authority in group situations
many peers view Non verbal expressions of power and dominance as manipulation for self gain
Their abuse can be disastrous
Men and women have different perceptions of Non verbal expressions of power and dominance
Nodding is misinterpreted in cross gender communication
women interpret a nod as a signal of understanding
men interpret a nod as a signal of agreement
small miscommunications and misinterpretations lead to disagreement and confrontation
Russel (as cited in Dunbar & Burgoon, 2005) describes, “the fundamental concept in social science is power, in the same way that energy is the fundamental concept in physics“. Power and dominance-submission are two key concepts in relationships, especially close relationships where individuals rely on one another to achieve their goals (Dunbar & Burgoon, 2005) and as such it is important to be able to identify indicators of dominance.
Power and dominance are different concepts yet share similarities. Power is the ability to influence behavior (Bachrach & Lawler; Berger; Burgoon et al.; Foa & Foa; French & Raven; Gray-Little & Burks; Henley; Olson & Cromwell; Rollins & Bahr, as cited in Dunbar & Burgoon, 2005) and may or may not be fully evident until challenged by an equal force (Huston, as cited in Dunbar & Burgoon, 2005). Unlike power, that may be latent, dominance is manifest reflecting individual (Komter, as cited in Dunbar & Burgoon, 2005), situational and relationship patterns where control attempts are either accepted or rejected (Rogers-Millar & Millar,as cited in Dunbar & Burgoon, 2005). Moskowitz, Suh, and Desaulniers (1994) mention two similar ways that people can relate to the world in interpersonal relationships: agency and communion. Agency includes status and is a continuum from assertiveness-dominance to passive-submissiveness – it can be measured by subtracting submissiveness from dominance. Communion is a second way to interact with others and includes love with a continuum from warm-agreeable to cold-hostile-quarrelsomeness. Power and dominance relate together in such a way that those with the greatest and least power typically do not assert dominance while those with more equal relationships make more control attempts Dunbar & Burgoon, 2005).
As one can see, power and dominance are important, intertwined, concepts that greatly impact relationships. In order to understand how dominance captures relationships one must understand the influence of gender and social roles while watching for verbal and nonverbal indicators of dominance.
Interactive Whiteboard Software
http://open-sankore.org/en/tutorials
Universal Interactive Whiteboard Software – top 3 so far
Saves files as Onenote, PDF, DOC, HTML.
Open Sankore. this is a little different but once you get used to it holy cow. This is one of the most feature-full IWB programs I have come across. It’s a regular IWB in many respects with a smaller gallery than most but nothing that can’t be expanded. But the widgets/apps that you can add are amazing.
Imagine being able to embed just about any file from the web
Imagine having a google map working within your whiteboard – wikipedia and wikictionary as well.
Imagine being able to have a page as big as you want (scrolling)
Imagine being able to embed working websites into the document
Imagine being able to create your own widgets with a just using HTML and CSS
I’d give this a go in a classroom – the interface is non standard but does make sense and auto saves your work until you want to export it. It has a nice extended desktop function for interactive pen displays.
Exports only as Sankore or PDF.
Read more: http://halljackson.blogspot.com/2012/05/universal-interactive-whiteboard.html#ixzz34a8Nr098