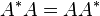Uncategorized – Page 7

dot product

Vector formulation

The law of cosines is equivalent to the formula

$vec bcdot vec c = Vert vec bVertVertvec cVertcos theta$

in the theory of vectors, which expresses the dot product of two vectors in terms of their respective lengths and the angle they enclose.

Fig. 10 — Vector triangle

Proof of equivalence. Referring to Figure 10, note that

$vec a=vec b-vec c,,$

and so we may calculate:

$begin{align} Vertvec aVert^2 & = Vertvec b - vec cVert^2 \ & = (vec b - vec c)cdot(vec b - vec c) \ & = Vertvec b Vert^2 + Vertvec c Vert^2 - 2 vec bcdotvec c. end{align}$

The law of cosines formulated in this notation states:

$Vertvec aVert^2 = Vertvec b Vert^2 + Vertvec c Vert^2 - 2 Vert vec bVertVertvec cVertcos(theta), ,$

which is equivalent to the above formula from the theory of vectors.

$A\cdot B=|A\|B|\cos \theta$ (by definition of dot product)

If you think of the length of the 3 vectors |A|,|B| and |B-A| as the lengths of the sides of a triangle, you can apply the law of cosines here too (To visualize this, draw the 2 vectors A and B onto a graph, now the vector from A to B will be given by B-A. The triangle formed by these 3 vectors is applied to the law of cosines for a triangle)
$C^2 = A^2 + B^2 - 2|A||B|\cos \theta$
In this case, we substitute: |B-A| for c, |A| for a, |B| for b
and we obtain:
$|B-A|^2 = |A|^2 + |B|^2 - 2 |A||B|\cos(\theta)$ (by law of cosines)

Remember now, that Theta is the angle between the 2 vectors A, B.
Notice the common term |A||B|cos(Theta) in both equations. We now equate equation (1) and (2), and obtain

$A\cdot B = (-(|B-A|^2) + |A|^2 + |B|^2) / 2$
and hence
$Acdot B =frac{1}{2} (-((B_x^2 - 2A_x B_x + A_x^2) + (B_y^2 - 2A_y B_y + A_y^2) + (B_z^2 - 2A_zB_z + A_z^2)) + A_x^2 + A_y^2 + A_z^2 + B_x^2 + B_y^2 + B_z^2)$
(by pythagorean length of a vector) and thus
$A\cdot B = A_xB_x + A_yB_y + A_zB_z$

Law of cosines

From Wikipedia, the free encyclopedia

This article is about the law of cosines in Euclidean geometry. For the cosine law of optics, see Lambert’s cosine law.

Figure 1 – A triangle. The angles α,β, and γ are respectively opposite the sides a, b, and c.

Trigonometry

History Usage Functions Generalized Inverse functions Further reading
Reference
Identities Exact constants Trigonometric tables
Laws and theorems
Law of sines Law of cosines Law of tangents Pythagorean theorem
Calculus
Trigonometric substitution Integrals of functions Derivatives of functions Integrals of inverse functions
v · d · e

In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) is a statement about a general triangle that relates the lengths of its sides to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states that

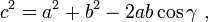
$c^2 = a^2 + b^2 - 2abcosgamma ,$

where γ denotes the angle contained between sides of lengths a and b and opposite the side of length c.

The law of cosines generalizes the Pythagorean theorem, which holds only for right triangles: if the angle γ is a right angle (of measure 90° or π/2 radians), then cos(γ) = 0, and thus the law of cosines reduces to

$c^2 = a^2 + b^2 ,$

The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known, and in computing the angles of a triangle if all three sides are known.

By changing which legs of the triangle play the roles of a, b, and c in the original formula, one discovers that the following two formulas also state the law of cosines:

$a^2 = b^2 + c^2 - 2bccosalpha,$

$b^2 = a^2 + c^2 - 2accosbeta,$

http://en.wikipedia.org/wiki/Law_of_cosines

cross product

http://www.physics.orst.edu/bridge/mathml/dot+cross.xhtml

Best approximation theorem

Theorem

Let X be an inner product space with induced norm, and $Asubseteq X$ a non-empty, complete convex subset. Then, for all $xin X$ , there exists a unique best approximation a₀ to x in A.

Proof

Suppose x = 0 (if not the case, consider A − {x} instead) and let $d=d(0,A)=inf_{ain A} ||a||$ . There exists a sequence (a_n) in Asuch that

$||a_n||to d$ .

We now prove that (a_n) is a Cauchy sequence. By the parallelogram rule, we get

$||frac{a_n-a_m}{2}||^2+||frac{a_n+a_m}{2}||^2=frac{1}{2}(||a_n||^2+||a_m||^2)$ .

Since A is convex, $frac{a_n+a_m}{2}in A$ so

$underset{m,nin mathbb N}{forall }; ||frac{a_n+a_m}{2}||geq d$ .

Hence

$||frac{a_n-a_m}{2}||^2leq frac{1}{2}(||a_n||^2+||a_m||^2)-d^2to 0$ as $m,nto infty$

which implies $||a_n-a_m||to 0$ as $m,nto infty$ . In other words, (a_n) is a Cauchy sequence. Since A is complete,

$underset{a_0in A}{exists }; a_nto a_0$ .

Since $a_0in A$ , $||a_0||geq d$ . Furthermore

$||a_0||leq ||a_0-a_n||+||a_n||to d$ as $nto infty$ ,

which proves | | a₀ | | = d. Existence is thus proved. We now prove uniqueness. Suppose there were two distinct best approximations a₀and a₀‘ to x (which would imply | | a₀ | | = | | a₀‘ | | = d). By the parallelogram rule we would have

$||frac{a_0+a_0'}{2}||^2+||frac{a_0-a_0'}{2}||^2=frac{1}{2}(||a_0||^2+||a_0'||^2)=d^2$ .

Then

$||frac{a_0+a_0'}{2}||^2<d^2$

which cannot happen since A is convex, and as such $frac{a_0+a_0'}{2}in A$ , which means $||frac{a_0+a_0'}{2}||^2geq d^2$ , thus completing the proof.

Rotation matrix

From Wikipedia, the free encyclopedia

In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example the matrix

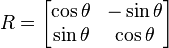
$R = begin{bmatrix} cos theta & -sin theta \ sin theta & cos theta \ end{bmatrix}$

rotates points in the xy–Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv (see below for details).

In two and three dimensions, rotation matrices are among the simplest algebraic descriptions of rotations, and are used extensively for computations in geometry, physics, and computer graphics. Though most applications involve rotations in two or three dimensions, rotation matrices can be defined for n-dimensional space.

Rotation matrices are always square, with real entries. Algebraically, a rotation matrix in n-dimensions is a n × n special orthogonal matrix, that is an orthogonal matrix whose determinant is 1:

$R^{T} = R^{-1}, det R = 1,$ .

The set of all rotation matrices forms a group, known as the rotation group or the special orthogonal group. It is a subset of the orthogonal group, which includes reflections and consists of all orthogonal matrices with determinant 1 or -1, and of the special linear group, which includes all volume-preserving transformations and consists of matrices with determinant 1.

http://en.wikipedia.org/wiki/Rotation_matrix

As in two dimensions a matrix can be used to rotate a point (x, y, z) to a point (x′, y′, z′). The matrix used is a 3 × 3 matrix,

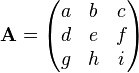
$mathbf{A} = begin{pmatrix} a & b & c \ d & e & f \ g & h & i end{pmatrix}$

This is multiplied by a vector representing the point to give the result

$mathbf{A} begin{pmatrix} x \ y \ z end{pmatrix} = begin{pmatrix} a & b & c \ d & e & f \ g & h & i end{pmatrix} begin{pmatrix} x \ y \ z end{pmatrix} = begin{pmatrix} x' \ y' \ z' end{pmatrix}$

The matrix A is a member of the three dimensional special orthogonal group, SO(3), that is it is an orthogonal matrix withdeterminant 1. That it is an orthogonal matrix means that its rows are a set of orthogonal unit vectors (so they are an orthonormal basis) as are its columns, making it easy to spot and check if a matrix is a valid rotation matrix. The determinant must be 1 as if it is -1 (the only other possibility for an orthogonal matrix) then the transformation given by it is a reflection, improper rotation or inversion in a point, i.e. not a rotation.

Matrices are often used for doing transformations, especially when a large number of points are being transformed, as they are a direct representation of the linear operator. Rotations represented in other ways are often converted to matrices before being used. They can be extended to represent rotations and transformations at the same time using Homogeneous coordinates. Transformations in this space are represented by 4 × 4 matrices, which are not rotation matrices but which have a 3 × 3 rotation matrix in the upper left corner.

The main disadvantage of matrices is that they are more expensive to calculate and do calculations with. Also in calculations wherenumerical instability is a concern matrices can be more prone to it, so calculations to restore orthonormality, which are expensive to do for matrices, need to be done more often.

Isometry

From Wikipedia, the free encyclopedia

For the mechanical engineering and architecture usage, see isometric projection. For isometry in differential geometry, seeisometry (Riemannian geometry).

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.

Isometries are often used in constructions where one space is embedded in another space. For instance, the completion of a metric space M involves an isometry from M into M’, a quotient set of the space of Cauchy sequences on M. The original space M is thus isometrically isomorphic to a subspace of a complete metric space, and it is usually identified with this subspace. Other embedding constructions show that every metric space is isometrically isomorphic to a closed subset of some normed vector space and that every complete metric space is isometrically isomorphic to a closed subset of some Banach space.

An isometric surjective linear operator on a Hilbert space is called a unitary operator.

http://en.wikipedia.org/wiki/Isometry

Unitary matrix

From Wikipedia, the free encyclopedia

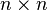
In mathematics, a unitary matrix is an $ntimes n$ complex matrix U satisfying the condition

$U^{dagger} U = UU^{dagger} = I_n,$

where I_n is the identity matrix in n dimensions and $U^{dagger}$ is the conjugate transpose (also called the Hermitian adjoint) of U. Note this condition says that a matrix U is unitary if and only if it has an inverse which is equal to its conjugate transpose $U^{dagger} ,$

$U^{-1} = U^{dagger} ,;$

A unitary matrix in which all entries are real is an orthogonal matrix. Just as an orthogonal matrix G preserves the (real) inner productof two real vectors,

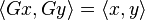
$langle Gx, Gy rangle = langle x, y rangle$

so also a unitary matrix U satisfies

$langle Ux, Uy rangle = langle x, y rangle$

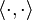for all complex vectors x and y, where $langlecdot,cdotrangle$ stands now for the standard inner product on $mathbb{C}^n$ .

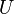If $U ,$ is an n by n matrix then the following are all equivalent conditions:

$U ,$ is unitary
$U^{dagger} ,$ is unitary
the columns of $U ,$ form an orthonormal basis of $mathbb{C}^n$ with respect to this inner product
the rows of $U ,$ form an orthonormal basis of $mathbb{C}^n$ with respect to this inner product
$U ,$ is an isometry with respect to the norm from this inner product
$U ,$ is a normal matrix with eigenvalues lying on the unit circle.

http://en.wikipedia.org/wiki/Unitary_matrix

Self-adjoint operator

From Wikipedia, the free encyclopedia

In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is one that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose. By the finite-dimensional spectral theorem such operators have an orthonormal basis in which the operator can be represented as a diagonal matrix with entries in the real numbers. In this article, we consider generalizations of this concept to operators on Hilbert spaces of arbitrary dimension.

Self-adjoint operators are used in functional analysis and quantum mechanics. In quantum mechanics their importance lies in the fact that in the Dirac–von Neumann formulation of quantum mechanics, physical observables such as position, momentum, angular momentum and spin are represented by self-adjoint operators on a Hilbert space. Of particular significance is the Hamiltonian

$H psi = V psi - frac{hbar^2}{2 m} nabla^2 psi$

which as an observable corresponds to the total energy of a particle of mass m in a real potential field V. Differential operators are an important class of unbounded operators.

The structure of self-adjoint operators on infinite dimensional Hilbert spaces essentially resembles the finite dimensional case, that is to say, operators are self-adjoint if and only if they are unitarily equivalent to real-valued multiplication operators. With suitable modifications, this result can be extended to possibly unbounded operators on infinite dimensional spaces. Since an everywhere defined self-adjoint operator is necessarily bounded, one needs be more attentive to the domain issue in the unbounded case. This is explained below in more detail.

http://en.wikipedia.org/wiki/Self-adjoint_operator

Spectral theorem

From Wikipedia, the free encyclopedia

In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can bediagonalized (that is, represented as a diagonal matrix in some basis). This concept of diagonalization is relatively straightforward for operators on finite-dimensional spaces, but requires some modification for operators on infinite-dimensional spaces. In general, the spectral theorem identifies a class of linear operators that can be modelled by multiplication operators, which are as simple as one can hope to find. In more abstract language, the spectral theorem is a statement about commutative C*-algebras. See also spectral theory for a historical perspective.

Examples of operators to which the spectral theorem applies are self-adjoint operators or more generally normal operators on Hilbert spaces.

The spectral theorem also provides a canonical decomposition, called the spectral decomposition, eigenvalue decomposition, or eigendecomposition, of the underlying vector space on which the operator acts.

In this article we consider mainly the simplest kind of spectral theorem, that for a self-adjoint operator on a Hilbert space. However, as noted above, the spectral theorem also holds for normal operators on a Hilbert space.

http://en.wikipedia.org/wiki/Spectral_theorem

Normal matrix

From Wikipedia, the free encyclopedia

A complex square matrix A is a normal matrix if

$A^*A=AA^*$

where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.

If A is a real matrix, then A*=A^T; it is normal if A^TA = AA^T.

Normality is a convenient test for diagonalizability: every normal matrix can be converted to a diagonal matrix by a unitary transform, and every matrix which can be made diagonal by a unitary transform is also normal, but finding the desired transform requires much more work than simply testing to see whether the matrix is normal.

The concept of normal matrices can be extended to normal operators on infinite dimensional Hilbert spaces and to normal elements in C*-algebras. As in the matrix case, normality means commutativity is preserved, to the extent possible, in the noncommutative setting. This makes normal operators, and normal elements of C*-algebras, more amenable to analysis.

http://en.wikipedia.org/wiki/Normal_matrix