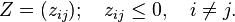the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from functions of one variable to functions on Banach spaces. The Fréchet derivative should be contrasted to the more general Gâteaux derivative which is a generalization of the classical directional derivative.
The Fréchet derivative has applications throughout mathematical analysis, and in particular to the calculus of variations and much of nonlinear analysis and nonlinear functional analysis. It has applications to nonlinear problems throughout the sciences.
Metzler matrix
a Metzler matrix is a matrix in which all the off-diagonal components are nonnegative (equal to or greater than zero)
Metzler matrices appear in stability analysis of time delayed differential equations and positive linear dynamical systems. Their properties can be derived by applying the properties of Nonnegative matrices to matrices of the form M + aI where M is a Metzler matrix.
P-matrix
a P-matrix is a complex square matrix with every principal minor > 0. A closely related class is that of P0-matrices, which are the closure of the class of P-matrices, with every principal minor 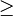 0.
0.
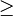 0.
0.
Spectra of P-matrices
By a theorem of Kellogg, the eigenvalues of P– and P0– matrices are bounded away from a wedge about the negative real axis as follows:
- If {u1,…,un} are the eigenvalues of an n-dimensional P-matrix, then
- If {u1,…,un},
 , i = 1,…,n are the eigenvalues of an n-dimensional P0-matrix, then
, i = 1,…,n are the eigenvalues of an n-dimensional P0-matrix, then
Notes
The class of nonsingular M-matrices is a subset of the class of P-matrices. More precisely, all matrices that are both P-matrices and Z-matrices are nonsingular M-matrices.
If the Jacobian of a function is a P-matrix, then the function is injective on any rectangular region of  .
.
 .
.A related class of interest, particularly with reference to stability, is that of P( − )-matrices, sometimes also referred to as N − P-matrices. A matrix A is a P( − )-matrix if and only if ( − A) is a P-matrix (similarly for P0-matrices). Since σ(A) = − σ( − A), the eigenvalues of these matrices are bounded away from the positive real axis.
References
- R. B. Kellogg, On complex eigenvalues of M and P matrices, Numer. Math. 19:170-175 (1972)
- Li Fang, On the Spectra of P– and P0-Matrices, Linear Algebra and its Applications 119:1-25 (1989)
- D. Gale and H. Nikaido, The Jacobian matrix and global univalence of mappings, Math. Ann. 159:81-93 (1965)
Z-matrix
the class of Z-matrices are those matrices whose off-diagonal entries are less than or equal to zero; that is, a Z-matrix Z satisfies
Note that this definition coincides precisely with that of a negated Metzler matrix or quasipositive matrix, thus the term quasinegative matrix appears from time to time in the literature, though this is rare and usually only in contexts where references to quasipositive matrices are made.
The Jacobian of a competitive dynamical system is a Z-matrix by definition. Likewise, if the Jacobian of a cooperative dynamical system is J, then (−J) is a Z-matrix.
Related classes are L-matrices, M-matrices, P-matrices, Hurwitz matrices and Metzler matrices. L-matrices have the additional property that all diagonal entries are greater than zero. M-matrices have several equivalent definitions, one of which is as follows: a Z-matrix is an M-matrix if it is nonsingular and its inverse is nonnegative. All matrices that are both Z-matrices and P-matrices are nonsingularM-matrices.
M-matrix
An M-matrix is a Z-matrix with eigenvalues whose real parts are positive. M-matrices are a subset of the class of P-matrices, and also of the class of inverse-positive matrices (i.e. matrices with inverses belonging to the class of positive matrices).[1]
A common characterization of an M-matrix is a non-singular square matrix with non-positive off-diagonal entries and all principal minors positive, but many equivalences are known. The name M-matrix was seemingly originally chosen by Alexander Ostrowski in reference to Hermann Minkowski.[2]
A symmetric M-matrix is sometimes called a Stieltjes matrix.
M-matrices arise naturally in some discretizations of differential operators, particularly those with a minimum/maximum principle, such as the Laplacian, and as such are well-studied in scientific computing.
The LU factors of an M-matrix are guaranteed to exist and can be stably computed without need for numerical pivoting, also have positive diagonal entries and non-positive off-diagonal entries. Furthermore, this holds even for incomplete LU factorization, where entries in the factors are discarded during factorization, providing useful preconditioners for iterative solution.
Gram–Schmidt process
the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly theEuclidean space Rn. The Gram–Schmidt process takes a finite, linearly independent set S = {v1, …, vk} for k ≤ n and generates an orthogonal set S′ = {u1, …, uk} that spans the same k-dimensional subspace of Rn as S.
The method is named for Jørgen Pedersen Gram and Erhard Schmidt but it appeared earlier in the work of Laplace and Cauchy. In the theory of Lie group decompositions it is generalized by theIwasawa decomposition.
The application of the Gram–Schmidt process to the column vectors of a full column rank matrix yields the QR decomposition (it is decomposed into an orthogonal and a triangular matrix).
The Gram–Schmidt process
We define the projection operator by
where 〈u, v〉 denotes the inner product of the vectors u and v. This operator projects the vector v orthogonally onto the vector u.
The Gram–Schmidt process then works as follows:
The sequence u1, …, uk is the required system of orthogonal vectors, and the normalized vectors e1, …, ek form an orthonormal set. The calculation of the sequence u1, …, uk is known as Gram–Schmidt orthogonalization, while the calculation of the sequence e1, …,ek is known as Gram–Schmidt orthonormalization as the vectors are normalized.
To check that these formulas yield an orthogonal sequence, first compute 〈u1, u2〉 by substituting the above formula for u2: we get zero. Then use this to compute 〈u1, u3〉 again by substituting the formula for u3: we get zero. The general proof proceeds bymathematical induction.
Geometrically, this method proceeds as follows: to compute ui, it projects vi orthogonally onto the subspace U generated by u1, …,ui−1, which is the same as the subspace generated by v1, …, vi−1. The vector ui is then defined to be the difference between vi and this projection, guaranteed to be orthogonal to all of the vectors in the subspace U.
The Gram–Schmidt process also applies to a linearly independent infinite sequence {vi}i. The result is an orthogonal (or orthonormal) sequence {ui}i such that for natural number n: the algebraic span of v1, …, vn is the same as that of u1, …, un.
If the Gram–Schmidt process is applied to a linearly dependent sequence, it outputs the 0 vector on the ith step, assuming that vi is a linear combination of v1, …, vi−1. If an orthonormal basis is to be produced, then the algorithm should test for zero vectors in the output and discard them because no multiple of a zero vector can have a length of 1. The number of vectors output by the algorithm will then be the dimension of the space spanned by the original inputs.
Numerical stability
When this process is implemented on a computer, the vectors uk are often not quite orthogonal, due to rounding errors. For the Gram–Schmidt process as described above (sometimes referred to as “classical Gram–Schmidt”) this loss of orthogonality is particularly bad; therefore, it is said that the (classical) Gram–Schmidt process is numerically unstable.
The Gram–Schmidt process can be stabilized by a small modification. Instead of computing the vector uk as
it is computed as
Each step finds a vector  orthogonal to
orthogonal to  . Thus
. Thus  is also orthogonalized against any errors introduced in computation of
is also orthogonalized against any errors introduced in computation of  . This approach (sometimes referred to as “modified Gram–Schmidt”) gives the same result as the original formula in exact arithmetic and introduces smaller errors in finite-precision arithmetic.
. This approach (sometimes referred to as “modified Gram–Schmidt”) gives the same result as the original formula in exact arithmetic and introduces smaller errors in finite-precision arithmetic.
 orthogonal to
orthogonal to  . Thus
. Thus  is also orthogonalized against any errors introduced in computation of
is also orthogonalized against any errors introduced in computation of  . This approach (sometimes referred to as “modified Gram–Schmidt”) gives the same result as the original formula in exact arithmetic and introduces smaller errors in finite-precision arithmetic.
. This approach (sometimes referred to as “modified Gram–Schmidt”) gives the same result as the original formula in exact arithmetic and introduces smaller errors in finite-precision arithmetic.
Algorithm
The following algorithm implements the stabilized Gram–Schmidt orthonormalization. The vectors v1, …, vk are replaced by orthonormal vectors which span the same subspace.
-
for j from 1 to k do
-
for i from 1 to j − 1 do
-
 (remove component in direction vi)
(remove component in direction vi)
-
- next i
-
 (normalize)
(normalize)
-
for i from 1 to j − 1 do
- next j
The cost of this algorithm is asymptotically 2nk2 floating point operations, where n is the dimensionality of the vectors (Golub & Van Loan 1996, §5.2.8)
UML Resources
Internet y la ciencia
Con solo una PC y conexión a Internet es posible participar en esfuerzos científicos de alcance global.
Explorar el universo
En el sitio www.galaxyzoo.org puedes ayudar a los astrónomos a explorar el universo. El sitio contiene un cuarto de millón de imágenes obtenidas por un telescopio robótico ( Sloan Digital Sky Survey) y voluntarios pueden ayudar a clasificar las imágenes.
La búsqueda de número primos
GIMPS provee programas que se pueden usar como screen savers y buscan números primos. Inclusive hay recompensa económica para motivar el desarrollo de esta tecnología a través de EFF Cooperative Computing Awards para el que encuentre primero:
- $50,000 por el primer número primo con más de 1,000,000 dígitos decimales ( Apr. 6, 2000).
- $100,000 por el primer número primo con más de 10,000,000 dígitos decimales. El 23 de agosto del 2008 la Electronic Frontier Foundation le concedió a GIMPS el premio ($100,000 Cooperative Computing Award) por el primo 45th del tipo Mersenne, 243,112,609-1, un número de 12,978,189 dígitos.
- $150,000 por el primer número primo con más de 100,000,000 dígitos decimales.
- $250,000 por el primer número primo con más de 1,000,000,000 dígitos decimales.
Nueva edición de las cátedras de Feynman
Reedición del clásico de clásicos. Es discutible su uso como libro de texto pero hasta los profesores se sentaban a oirlo.
Introducción a la electrodinámica cuántica
Solo Richard P. Feynman puede siquiera intentar presentar este material a una audiencia general.
QED: The Strange Theory of Light and Matter (Princeton Science Library)