Self-adjoint operator
From Wikipedia, the free encyclopedia
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is one that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose. By the finite-dimensional spectral theorem such operators have an orthonormal basis in which the operator can be represented as a diagonal matrix with entries in the real numbers. In this article, we consider generalizations of this concept to operators on Hilbert spaces of arbitrary dimension.
Self-adjoint operators are used in functional analysis and quantum mechanics. In quantum mechanics their importance lies in the fact that in the Dirac–von Neumann formulation of quantum mechanics, physical observables such as position, momentum, angular momentum and spin are represented by self-adjoint operators on a Hilbert space. Of particular significance is the Hamiltonian
which as an observable corresponds to the total energy of a particle of mass m in a real potential field V. Differential operators are an important class of unbounded operators.
The structure of self-adjoint operators on infinite dimensional Hilbert spaces essentially resembles the finite dimensional case, that is to say, operators are self-adjoint if and only if they are unitarily equivalent to real-valued multiplication operators. With suitable modifications, this result can be extended to possibly unbounded operators on infinite dimensional spaces. Since an everywhere defined self-adjoint operator is necessarily bounded, one needs be more attentive to the domain issue in the unbounded case. This is explained below in more detail.


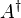 , then the Hermitian property can be written concisely as
, then the Hermitian property can be written concisely as