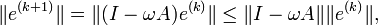Tag: method

Power iteration

Power iteration

From Wikipedia, the free encyclopedia
In mathematics, the power iteration is an eigenvalue algorithm: given a matrix A, the algorithm will produce a number λ (theeigenvalue) and a nonzero vector v (the eigenvector), such that Av = λv.
The power iteration is a very simple algorithm. It does not compute a matrix decomposition, and hence it can be used when A is a very large sparse matrix. However, it will find only one eigenvalue (the one with the greatest absolute value) and it may converge only slowly.

Arnoldi iteration

Arnoldi iteration

From Wikipedia, the free encyclopedia
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general (possibly non-Hermitian) matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E. Arnoldi in 1951.
The term iterative method, used to describe Arnoldi, can perhaps be somewhat confusing. Note that all general eigenvalue algorithms must be iterative. This is not what is referred to when we say Arnoldi is an iterative method. Rather, Arnoldi belongs to a class of linear algebra algorithms (based on the idea of Krylov subspaces) that give a partial result after a relatively small number of iterations. This is in contrast to so-called direct methods, which must complete to give any useful results.
Arnoldi iteration is a typical large sparse matrix algorithm: It does not access the elements of the matrix directly, but rather makes the matrix map vectors and makes its conclusions from their images. This is the motivation for building the Krylov subspace.

Krylov subspace

Krylov subspace

From Wikipedia, the free encyclopedia
In linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspacespanned by the images of b under the first r powers of A (starting from A0 = I), that is,
mathcal{K}_r(A,b) = operatorname{span} , { b, Ab, A^2b, ldots, A^{r-1}b }. ,
It is named after Russian applied mathematician and naval engineer Alexei Krylov, who published a paper on this issue in 1931.[1]
Modern iterative methods for finding one (or a few) eigenvalues of large sparse matrices or solving large systems of linear equations avoid matrix-matrix operations, but rather multiply vectors by the matrix and work with the resulting vectors. Starting with a vector, b, one computes Ab, then one multiplies that vector by A to find A2b and so on. All algorithms that work this way are referred to as Krylov subspace methods; they are among the most successful methods currently available in numerical linear algebra.
Because the vectors tend very quickly to become almost linearly dependent, methods relying on Krylov subspace frequently involve some orthogonalization scheme, such as Lanczos iteration for Hermitian matrices or Arnoldi iteration for more general matrices.
The best known Krylov subspace methods are the Arnoldi, Lanczos, Conjugate gradient, GMRES (generalized minimum residual),BiCGSTAB (biconjugate gradient stabilized), QMR (quasi minimal residual), TFQMR (transpose-free QMR), and MINRES (minimal residual) methods.

References

  1. ^ Mike Botchev (2002). “A.N.Krylov, a short biography”.

Conjugate gradient method

Conjugate gradient method

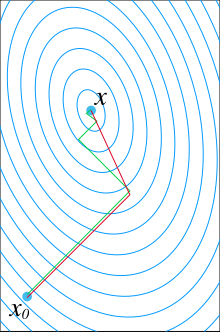
From Wikipedia, the free encyclopedia

A comparison of the convergence ofgradient descent with optimal step size (in green) and conjugate gradient (in red) for minimizing a quadratic function associated with a given linear system. Conjugate gradient, assuming exact arithmetics, converges in at most n steps where n is the size of the matrix of the system (here n=2).

In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix issymmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too large to be handled by direct methods such as the Cholesky decomposition. Such systems often arise when numerically solvingpartial differential equations.
The conjugate gradient method can also be used to solve unconstrained optimizationproblems such as energy minimization.
The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear equations.

Successive over-relaxation

Successive over-relaxation

From Wikipedia, the free encyclopedia
In numerical linear algebra, the method of successive over-relaxation (SOR) is a variant of the Gauss–Seidel method for solving alinear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process. It was devised simultaneously by David M. Young and by H. Frankel in 1950 for the purpose of automatically solving linear systems on digital computers. Over-relaxation methods had been used before the work of Young and Frankel. For instance, the method of Lewis Fry Richardson, and the methods developed by R. V. Southwell. However, these methods were designed for computation by human calculators, and they required some expertise to ensure convergence to the solution which made them inapplicable for programming on digital computers. These aspects are discussed in the thesis of David M. Young.[1]

Gauss–Seidel method

Gauss–Seidel method

From Wikipedia, the free encyclopedia
In numerical linear algebra, the Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method used to solve a linear system of equations. It is named after the German mathematicians Carl Friedrich Gauss and Philipp Ludwig von Seidel, and is similar to the Jacobi method. Though it can be applied to any matrix with non-zero elements on the diagonals, convergence is guaranteed if the matrix is either diagonally dominant, or symmetric and positive definite.

Jacobi method

Jacobi method

From Wikipedia, the free encyclopedia
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process is then iterated until it converges. This algorithm is a stripped-down version of the Jacobi transformation method of matrix diagonalization. The method is named after German mathematician Carl Gustav Jakob Jacobi.

Chebyshev iteration method


An iterative algorithm for finding a solution to a linear equation
(1)

that takes account of information about the inclusion of  — the spectrum of the operator  — in a certain set , and uses the properties and parameters of those polynomials that deviate least from zero on  and are equal to 1 at 0.

The most well-developed Chebyshev iteration method is obtained when in (1),  is a linear self-adjoint operator and , where  are the boundary points of the spectrum; then the Chebyshev iteration method uses the properties of the Chebyshev polynomials of the first kind, . For this case one considers two types of Chebyshev iteration methods:
(2)
(3)

in which for a given  one obtains a sequence  as . In (2) and (3)  and  are the numerical parameters of the method. If , then the initial error  and the error at the -th iteration  are related by the formula

where

(4)

The polynomials  are calculated using the parameters of each of the methods (2), (3): for method(2)

(5)

where  are the elements of the permutation , while for method (3)they are calculated from the recurrence relations

(6)

Here

The methods (2) and (3) can be optimized on the class of problems for which  by choosing the parameters such that  in (4) is the polynomial least deviating from zero on . It was proved in 1881 by P.L. Chebyshev that this is the polynomial
(7)

where . Then

(8)

where

Substituting (7) for  in (6), the parameters  of the method (3) are determined:
(9)

where

(10)

Thus, computing  and  by the formulas (9) and (10), one obtains the Chebyshev iteration method (3) for which  is optimally small for each .
To optimize (2) for a given , the parameters  are chosen corresponding to the permutation in formula (5) in such a way that (7) holds, that is,
(11)

Then after  iterations, inequality (8) holds for .

An important problem for small  is the question of the stability of the method (2), (5), (11). An imprudent choice of  may lead to a catastrophic increase in  for some , to the loss of significant figures, or to an increase in the rounding-off errors allowed on intermediate iteration. There exist algorithms that mix the parameters in (11) and guarantee the stability of the calculations: for  see Iteration algorithm; and for  one of the algorithms for constructing  is as follows. Let , and suppose that  has been constructed, then
(12)

There exists a class of methods (2) — the stable infinitely repeated optimal Chebyshev iteration methods — that allows one to repeat the method (2), (5), (11) after  iterations in such a way that it is stable and such that it becomes optimal again for some sequence . For the case , it is clear from the formula
(13)

that  agrees with (11). If after  iterations one repeats the iteration (2), (5), (11) further, taking for  in (11) the  values

(14)

then once again one obtains a Chebyshev iteration method after  iterations. To ensure stability, the set(14) is decomposed into two sets: in the -th set, , one puts the  for which  is a root of the -th bracket in (13); within each of the subsets the  are permuted according to the permutation . For  one substitutes elements of the first set in (5), (11), and for  one uses the second subset; the permutation  is defined in the same way. Continuing in an analogous way the process of forming parameters, one obtains an infinite sequence , uniformly distributed on , called a -sequence, for which the method (2) becomes optimal with  and

(15)

The theory of the Chebyshev iteration methods (2), (3) can be extended to partial eigen value problems. Generalizations also exist to a certain class of non-self-adjoint operators, when  lies in a certain interval or within a certain domain of special shape (in particular, an ellipse); when information is known about the distribution of the initial error; or when the Chebyshev iteration method is combined with the method of conjugate gradients.
One of the effective methods of speeding up to the convergence of the iterations (2), (3) is a preliminary transformation of equation (1) to an equivalent equation of the form

and the application of the Chebyshev iteration method to this equation. The operator  is defined by taking account of two facts: 1) the algorithm for computing a quantity of the form  should not be laborious; and 2)  should lie in a set that ensures the fast convergence of the Chebyshev iteration method.

References

[1]  G.I. Marchuk,   V.I. Lebedev,   “Numerical methods in the theory of neutron transport” , Harwood  (1986)  (Translated from Russian)
[2]  N.S. Bakhvalov,   “Numerical methods: analysis, algebra, ordinary differential equations” , MIR  (1977)  (Translated from Russian)
[3]  G.I. Marchuk,   “Methods of numerical mathematics” , Springer  (1982)  (Translated from Russian)
[4]  A.A. Samarskii,   “Theorie der Differenzverfahren” , Akad. Verlagsgesell. Geest u. Portig K.-D.  (1984)  (Translated from Russian)
[5a]  V.I. Lebedev,   S.A. Finogenov,   “The order of choices of the iteration parameters in the cyclic Chebyshev iteration method”  Zh. Vychisl. Mat. i Mat. Fiz. , 11 : 2  (1971)  pp. 425–438  (In Russian)
[5b]  V.I. Lebedev,   S.A. Finogenov,   “Solution of the problem of parameter ordering in Chebyshev iteration methods”  Zh. Vychisl. Mat. i Mat. Fiz , 13 : 1  (1973)  pp. 18–33  (In Russian)
[5c]  V.I. Lebedev,   S.A. Finogenov,   “The use of ordered Chebyshev parameters in iteration methods”  Zh. Vychisl. Mat. i Mat. Fiz. , 16 : 4  (1976)  pp. 895–907  (In Russian)
[6a]  V.I. Lebedev,   “Iterative methods for solving operator equations with spectrum located on several segments”  Zh. Vychisl. Mat. i Mat. Fiz. , 9 : 6  (1969)  pp. 1247–1252  (In Russian)
[6b]  V.I. Lebedev,   “Iteration methods for solving linear operator equations, and polynomials deviating least from zero” , Mathematical analysis and related problems in mathematics , Novosibirsk  (1978)  pp. 89–108  (In Russian)

Comments

In the Western literature the method (2), (5), (11) is known as the Richardson method of first degree [a2]or, more widely used, the Chebyshev semi-iterative method of first degree. The method goes back to an early paper of L.F. Richardson , where the method (2), (5) was already proposed. However, Richardson did not identify the zeros  of  with the zeros of (shifted) Chebyshev polynomials as done in (11), but (less sophisticatedly) sprinkled them uniformly over the interval . The use of Chebyshev polynomials seems to be proposed for the first time in [a1] and [a3].
The  “stable infinitely repeated optimal Chebyshev iteration methods”  outlined above are based on the identity , which immediately leads to the factorization

This formula has already been used in [a1] in the numerical determination of fundamental modes.

The method (3), (9) is known as Richardson’s method or Chebyshev’s semi-iterative method of second degree. It was suggested in [a9] and turns out to be completely stable; thus, at the cost of an extra storage array the instability problems associated with the first-degree process are avoided.
As to the choice of the transformation operator  (called  “preconditioningpreconditioning” ), an often used  “preconditionerpreconditioner”  is the so-called SSOR matrix (Symmetric Successive Over-Relaxation matrix) proposed in [a8].
Introductions to the theory of Chebyshev semi-iterative methods are provided by [a2] and [a3]. An extensive analysis can be found in [a10], Chapt. 5 and in [a4]. In this work the spectrum of the operator  is assumed to be real. An analysis of the case where the spectrum is not real can be found in [a5].
Instead of using minimax polynomials, one may consider integral measures for  “minimizing”   on . This leads to the theory of kernel polynomials introduced in [a9] and extended in [a11], Chapt. 5.
Iterative methods as opposed to direct methods (cf. Direct method) only make sense when the matrix is sparse (cf. Sparse matrix). Moreover, their versatility depends on how large an error  is tolerated; often other errors, e.g., truncation errors in discretized systems of partial differential equations, are more dominant.
When no information about the eigen structure of  is available, or in the non-self-adjoint case, it is often preferable to use the method of conjugate gradients (cf. Conjugate gradients, method of). Numerical algorithms based on the latter method combined with incomplete factorization have proven to be one of the most efficient ways to solve linear problems up to now (1987).

References

[a1]  D.A. Flanders,   G. Shortley,   “Numerical determination of fundamental modes”  J. Appl. Physics, 21  (1950)  pp. 1326–1332
[a2]  G.E. Forsythe,   W.R. Wasow,   “Finite difference methods for partial differential equations” , Wiley  (1960)
[a3]  G.H. Golub,   C.F. van Loan,   “Matrix computations” , North Oxford Acad.  (1983)
[a4]  G.H. Golub,   R.S. Varga,   “Chebyshev semi-iterative methods, successive over-relaxation methods and second-order Richardson iterative methods I, II”  Num. Math. , 3  (1961)  pp. 147–156; 157–168
[a5]  T.A. Manteuffel,   “The Tchebychev iteration for nonsymmetric linear systems”  Num. Math. , 28 (1977)  pp. 307–327
[a6a]  L.F. Richardson,   “The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam”  Philos. Trans. Roy. Soc. London Ser. A , 210  (1910)  pp. 307–357
[a6b]  L.F. Richardson,   “The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam”  Proc. Roy. Soc. London Ser. A , 83  (1910)  pp. 335–336
[a7]  G. Shortley,   “Use of Tchebycheff-polynomial operators in the numerical solution of boundary-value problems”  J. Appl. Physics , 24  (1953)  pp. 392–396
[a8]  J.W. Sheldon,   “On the numerical solution of elliptic difference equations”  Math. Tables Aids Comp. , 9  (1955)  pp. 101–112
[a9]  E.L. Stiefel,   “Kernel polynomials in linear algebra and their numerical applications” , Appl. Math. Ser. , 49 , Nat. Bur. Standards  (1958)
[a10]  R.S. Varga,   “Matrix iterative analysis” , Prentice-Hall  (1962)
[a11]  E.L. Wachspress,   “Iterative solution of elliptic systems, and applications to the neutron diffusion equations of nuclear physics” , Prentice-Hall  (1966)

Extremal polynomials with application to Richardson iteration for indefinite linear systems (Technical summary report / Mathematics Research Center, University of Wisconsin–Madison)

Modified Richardson iteration

Modified Richardson iteration is an iterative method for solving a system of linear equations. Richardson iteration was proposed by Lewis Richardson in his work dated 1910. It is similar to the Jacobiand Gauss–Seidel method.
We seek the solution to a set of linear equations, expressed in matrix terms as
A x = b.,
The Richardson iteration is
x^{(k+1)} = x^{(k)} + omega left( b - A x^{(k)} right),
where ω is a scalar parameter that has to be chosen such that the sequence x(k) converges.
It is easy to see that the method is correct, because if it converges, then x^{(k+1)} approx x^{(k)} and x(k) has to approximate a solution of Ax = b.


Convergence

Subtracting the exact solution x, and introducing the notation for the error e^{(k)} approx x^{(k)}-x, we get the equality for the errors
e(k + 1) = e(k) − ωAe(k) = (I − ωA)e(k).
Thus,
|e^{(k+1)}| = |(I-omega A) e^{(k)}|leq |I-omega A| |e^{(k)}|,
for any vector norm and the corresponding induced matrix norm. Thus, if |I-omega A|<1 the method convergences.
Suppose that A is diagonalizable and that (λj,vj) are the eigenvalues and eigenvectors of A. The error converges to 0 if | 1 − ωλj | < 1 for all eigenvalues λj. If, e.g., all eigenvalues are positive, this can be guaranteed if ω is chosen such that 0 < ω < 2 / λmax(A). The optimal choice, minimizing all | 1 − ωλj | , is ω = 2 / (λmin(A) + λmax(A)), which gives the simplest Chebyshev iteration.
If there are both positive and negative eigenvalues, the method will diverge for any ω if the initial error e(0) has nonzero components in the corresponding eigenvectors.


References