From Wikipedia, the free encyclopedia

In mathematics, a Hermitian matrix (or self-adjoint matrix) is a square matrix with complex entries that is equal to its ownconjugate transpose – that is, the element in the i-th row and j-th column is equal to the complex conjugate of the element in the j-th row and i-th column, for all indices i and j:

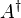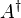If the conjugate transpose of a matrix A is denoted by , then the Hermitian property can be written concisely as

Hermitian matrices can be understood as the complex extension of real symmetric matrices.

Hermitian matrices are named after Charles Hermite, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of having eigenvalues always real.