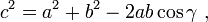trigonometry

Vector formulation

The law of cosines is equivalent to the formula

$vec bcdot vec c = Vert vec bVertVertvec cVertcos theta$

in the theory of vectors, which expresses the dot product of two vectors in terms of their respective lengths and the angle they enclose.

Fig. 10 — Vector triangle

Proof of equivalence. Referring to Figure 10, note that

$vec a=vec b-vec c,,$

and so we may calculate:

$begin{align} Vertvec aVert^2 & = Vertvec b - vec cVert^2 \ & = (vec b - vec c)cdot(vec b - vec c) \ & = Vertvec b Vert^2 + Vertvec c Vert^2 - 2 vec bcdotvec c. end{align}$

The law of cosines formulated in this notation states:

$Vertvec aVert^2 = Vertvec b Vert^2 + Vertvec c Vert^2 - 2 Vert vec bVertVertvec cVertcos(theta), ,$

which is equivalent to the above formula from the theory of vectors.

$A\cdot B=|A\|B|\cos \theta$ (by definition of dot product)

If you think of the length of the 3 vectors |A|,|B| and |B-A| as the lengths of the sides of a triangle, you can apply the law of cosines here too (To visualize this, draw the 2 vectors A and B onto a graph, now the vector from A to B will be given by B-A. The triangle formed by these 3 vectors is applied to the law of cosines for a triangle)
$C^2 = A^2 + B^2 - 2|A||B|\cos \theta$
In this case, we substitute: |B-A| for c, |A| for a, |B| for b
and we obtain:
$|B-A|^2 = |A|^2 + |B|^2 - 2 |A||B|\cos(\theta)$ (by law of cosines)

Remember now, that Theta is the angle between the 2 vectors A, B.
Notice the common term |A||B|cos(Theta) in both equations. We now equate equation (1) and (2), and obtain

$A\cdot B = (-(|B-A|^2) + |A|^2 + |B|^2) / 2$
and hence
$Acdot B =frac{1}{2} (-((B_x^2 - 2A_x B_x + A_x^2) + (B_y^2 - 2A_y B_y + A_y^2) + (B_z^2 - 2A_zB_z + A_z^2)) + A_x^2 + A_y^2 + A_z^2 + B_x^2 + B_y^2 + B_z^2)$
(by pythagorean length of a vector) and thus
$A\cdot B = A_xB_x + A_yB_y + A_zB_z$

Law of cosines

From Wikipedia, the free encyclopedia

This article is about the law of cosines in Euclidean geometry. For the cosine law of optics, see Lambert’s cosine law.

Figure 1 – A triangle. The angles α,β, and γ are respectively opposite the sides a, b, and c.

Trigonometry

History Usage Functions Generalized Inverse functions Further reading
Reference
Identities Exact constants Trigonometric tables
Laws and theorems
Law of sines Law of cosines Law of tangents Pythagorean theorem
Calculus
Trigonometric substitution Integrals of functions Derivatives of functions Integrals of inverse functions
v · d · e

In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) is a statement about a general triangle that relates the lengths of its sides to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states that

$c^2 = a^2 + b^2 - 2abcosgamma ,$

where γ denotes the angle contained between sides of lengths a and b and opposite the side of length c.

The law of cosines generalizes the Pythagorean theorem, which holds only for right triangles: if the angle γ is a right angle (of measure 90° or π/2 radians), then cos(γ) = 0, and thus the law of cosines reduces to

$c^2 = a^2 + b^2 ,$

The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known, and in computing the angles of a triangle if all three sides are known.

By changing which legs of the triangle play the roles of a, b, and c in the original formula, one discovers that the following two formulas also state the law of cosines:

$a^2 = b^2 + c^2 - 2bccosalpha,$

$b^2 = a^2 + c^2 - 2accosbeta,$

http://en.wikipedia.org/wiki/Law_of_cosines