Normal matrix
From Wikipedia, the free encyclopedia
where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.
If A is a real matrix, then A*=AT; it is normal if ATA = AAT.
Normality is a convenient test for diagonalizability: every normal matrix can be converted to a diagonal matrix by a unitary transform, and every matrix which can be made diagonal by a unitary transform is also normal, but finding the desired transform requires much more work than simply testing to see whether the matrix is normal.
The concept of normal matrices can be extended to normal operators on infinite dimensional Hilbert spaces and to normal elements in C*-algebras. As in the matrix case, normality means commutativity is preserved, to the extent possible, in the noncommutative setting. This makes normal operators, and normal elements of C*-algebras, more amenable to analysis.
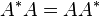
Your site does not show up appropriately on my i phone – you may wanna try and repair that