What is the computational complexity of inverting an nxn matrix? (In
general, not special cases such as a triangular matrix.)
Gaussian Elimination leads to O(n^3) complexity. The usual way to
count operations is to count one for each "division" (by a pivot) and
one for each "multiply-subtract" when you eliminate an entry.
Here's one way of arriving at the O(n^3) result:
At the beginning, when the first row has length n, it takes n
operations to zero out any entry in the first column (one division,
and n-1 multiply-subtracts to find the new entries along the row
containing that entry. To get the first column of zeroes therefore
takes n(n-1) operations.
In the next column, we need (n-1)(n-2) operations to get the second
column zeroed out.
In the third column, we need (n-2)(n-3) operations.
The sum of all of these operations is:
n n n n(n+1)(2n+1) n(n+1)
SUM i(i-1) = SUM i^2 - SUM i = ------------ - ------
i=1 i=1 i=1 6 2
which goes as O(n^3). To finish the operation count for Gaussian
Elimination, you'll need to tally up the operations for the process
of back-substitution (you can check that this doesn't affect the
leading order of n^3).
You might think that the O(n^3) complexity is optimal, but in fact
there exists a method (Strassen's method) that requires only
O(n^log_2(7)) = O(n^2.807...) operations for a completely general
matrix. Of course, there is a constant C in front of the n^2.807. This
constant is not small (between 4 and 5), and the programming of
Strassen's algorithm is so awkward, that often Gaussian Elimination is
still the preferred method.
Even Strassen's method is not optimal. I believe that the current
record stands at O(n^2.376), thanks to Don Coppersmith and Shmuel
Winograd. Here is a Web page that discusses these methods:
Fast Parallel Matrix Multiplication - Strategies for Practical
Hybrid Algorithms - Erik Ehrling
http://www.f.kth.se/~f95-eeh/exjobb/background.html
These methods exploit the close relation between matrix inversion and
matrix multiplication (which is also an O(n^3) task at first glance).
I hope this helps!
- Doctor Douglas, The Math Forum
http://mathforum.org/dr.math/
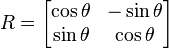
 .
.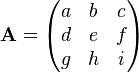


 is the
is the 


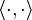 stands now for the standard
stands now for the standard  .
.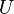 is an n by n matrix then the following are all equivalent conditions:
is an n by n matrix then the following are all equivalent conditions: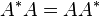

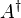 , then the Hermitian property can be written concisely as
, then the Hermitian property can be written concisely as