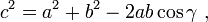Law of cosines
From Wikipedia, the free encyclopedia
This article is about the law of cosines in Euclidean geometry. For the cosine law of optics, see Lambert’s cosine law.
In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) is a statement about a general triangle that relates the lengths of its sides to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states that
where γ denotes the angle contained between sides of lengths a and b and opposite the side of length c.
The law of cosines generalizes the Pythagorean theorem, which holds only for right triangles: if the angle γ is a right angle (of measure 90° or π/2 radians), then cos(γ) = 0, and thus the law of cosines reduces to
The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known, and in computing the angles of a triangle if all three sides are known.
By changing which legs of the triangle play the roles of a, b, and c in the original formula, one discovers that the following two formulas also state the law of cosines: